北理工在隨機偏微分方程研究領域取得重要進展
發布日期:2019-10-10 供稿:數學與統計學院
編輯:陶思遠 審核:張楊 閱讀次數:
最近幾十年,隨機偏微分方程的理論研究一直是數學科學的研究熱點。當驅動噪聲是時空白噪聲(分布)時,解的良定性是一個困擾多年的公開問題。主要的困難在于當噪聲是奇異噪聲時,對應方程解的正則性較差,使得解的乘積或者解求導之后的乘積無法通過數學嚴格描述。英國帝國理工大學的Martin Hairer教授首先想到用粗糙路徑(rough path)理論來處理一維空間的奇異性,并用這套方法構造了一維KPZ方程的解。之后, Hairer教授提出了一種高維空間新的理論:正則結構理論(regularity structure theory),給出了在次臨界條件下帶有奇異噪聲的隨機偏微分方程良定的一般方法,這是隨機偏微分方程領域的重大發展。Hairer教授因為這一結果獲得了2014年Fields獎。同時,Gubinelli,Imkeller和Perkowski基于被控制的粗糙路徑(controlled rough path)和調和分析中仿積的思想提出了擬控制分布(paracontrolled distribution)的方法。這個方法也可以用來研究奇異的隨機偏微分方程。Gubinelli教授也因為這個方法在2018年國際數學家大會做45分鐘報告。這兩種方法的提出是隨機分析領域的最新發展。
北理工朱蓉禪副教授及其合作者基于上述兩種方法研究帶有奇異噪聲的隨機偏微分方程,具體研究了時空白噪聲驅動的三維Navier-Stokes方程、與量子場論中基本模型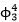 場相關的
場相關的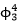 動力模型,取得了一系列的研究成果。相關結果發表在國際數學一流期刊《The annals of probability》《Journal of differential equations》等上。這些結果多次被Hairer、Gubinelli等數學家引用。
動力模型,取得了一系列的研究成果。相關結果發表在國際數學一流期刊《The annals of probability》《Journal of differential equations》等上。這些結果多次被Hairer、Gubinelli等數學家引用。
朱蓉禪副教授及其合作者結合狄氏型理論和上述兩種理論的最新發展進一步研究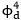 動力模型,他們結合上述兩種理論的最新發展解決了
動力模型,他們結合上述兩種理論的最新發展解決了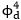 動力模型狄氏型長期未解決的問題,并對
動力模型狄氏型長期未解決的問題,并對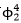 場給出刻畫,相關工作發表于國際數學一流期刊在《Communication in mathematical physics》《Journal of functional analysis》等。這些結果受到Hairer、Gubinelli等數學家的高度關注。Gubinelli教授在2018國際數學家大會上引用了朱蓉禪副教授及其合作者的最新研究結果。
場給出刻畫,相關工作發表于國際數學一流期刊在《Communication in mathematical physics》《Journal of functional analysis》等。這些結果受到Hairer、Gubinelli等數學家的高度關注。Gubinelli教授在2018國際數學家大會上引用了朱蓉禪副教授及其合作者的最新研究結果。
基于上述創新研究和一流學術成果,2019年朱蓉禪副教授獲批國家自然科學基金優秀青年科學基金。
分享到:
